2024-07-02
清华大学交叉信息研究院邓东灵研究组与浙江大学物理学院王浩华、宋超研究组等合作,在超导系统中首次制备了斐波那契非阿贝尔拓扑态并实现了斐波那契任意子的编织操作。该成果论文《量子处理器上斐波那契任意子的非阿贝尔编织》(Non-Abelian braiding of Fibonacci anyons with a superconducting processor)近日以Article的形式在《自然物理》(Nature Physics)杂志发表。

图1 斐波那契任意子编织示意图
自然界中常见的基础粒子分为玻色子和费米子两种,交换两个基础粒子的位置会导致系统波函数产生+1(玻色子,如光子)或-1(费米子,如电子)的相位。这是由于在三维空间中,粒子A绕粒子B一圈(等价于交换位置两次)的环路可以在不经过粒子B的情况下连续变形至消失。这限制了系统在粒子交换两次后必须回到最初的量子态,因此每交换一次系统波函数只能产生+1或-1的相因子,相应的粒子被称为玻色子或费米子,满足玻色-爱因斯坦或费米-狄拉克统计规律。而在二维空间中,粒子A绕粒子B一圈的环路无法在不经过粒子B的情况下连续变形至消失,因此没有粒子交换两次后必须回到最初的量子态的限制。在此情形下,粒子的交换可以产生任意的相位,这样的粒子被称作阿贝尔任意子(Anyon),其交换位置的过程被称作编织(braiding)。更一般地,如果系统基态存在简并,交换两个粒子甚至可以改变系统波函数的振幅,导致系统整体的幺正演化而非仅获得一个全局相位。这种粒子被称为非阿贝尔任意子。
非阿贝尔任意子的研究具有重要基础理论意义和潜在应用价值。此类粒子满足非阿贝尔统计规律,是与传统玻色子和费米子有着根本不同奇异粒子。非阿贝尔任意子也是拓扑量子计算的基石。在拓扑量子计算中,量子门由非阿贝尔任意子的编织实现,计算结果的测量则由任意子的融合(fusion)完成。任意子的拓扑性质使得这种量子计算机天生对局域错误免疫,提供了硬件层面的容错量子计算方案。
尽管存在多种理论方案,非阿贝尔任意子的实验实现十分困难,直到近年来才出现在量子处理器上模拟非阿贝尔任意子的工作。然而之前所有模拟的非阿贝尔任意子其编织操作所对应的量子门均不具备通用量子计算的能力。而斐波那契任意子则拥有更加复杂的统计性质,其实验实现更为困难。斐波那契任意子量子维度为黄金分割数1.618,与数学中的斐波那契序列息息相关(见图1)。其编织能实现任意量子门,可以用于构建通用的容错量子计算机。
实验制备斐波那契非阿贝尔拓扑态以及实现斐波那契任意子的编织操作被广泛认为极为困难。本实验采用弦网凝聚模型,通过几何变换使得超导量子芯片方形格子上的量子比特与弦网模型中蜂窝形状的“弦”相吻合(见图2)。在该模型中,系统哈密顿量由所有涡旋算符Qv和所有块算符Bp之和构成,基态中所有的弦均为闭合,而激发态中斐波那契任意子分布在开弦的两端(见图2)。本实验使用了27个超导量子比特,单(双)比特门精度为99.96%(99.5%),通过115层量子线路制备了系统基态。
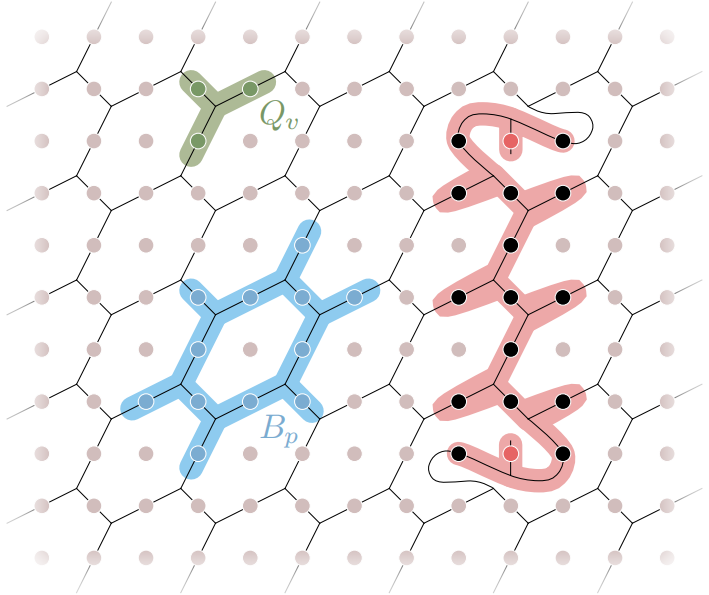
图2 正方格子上的弦网模型
在制备基态之后,实验通过将系统分成不同区域的方法测量了拓扑纠缠熵,所得结果与理论预言吻合。在此基础上,实验通过弦算符操作产生了两对斐波那契任意子并展示了他们的编织操作(图3)。实验设计了多种不同的编织次序来测试斐波那契任意子的特性(见图3a),分别为:(i)斐波那契任意子与其反粒子湮灭;(ii)编织改变融合结果;(iii)和(iv)融合结果相同验证Yang-Baxter方程;(v)测量斐波那契任意子的量子维度。实验所得结果均与理论预测吻合得很好(见图3b),其中根据编制次序(v)的实验结果所得的斐波那契任意子量子维度为1.598,十分接近理论预言的黄金分割率1.618。
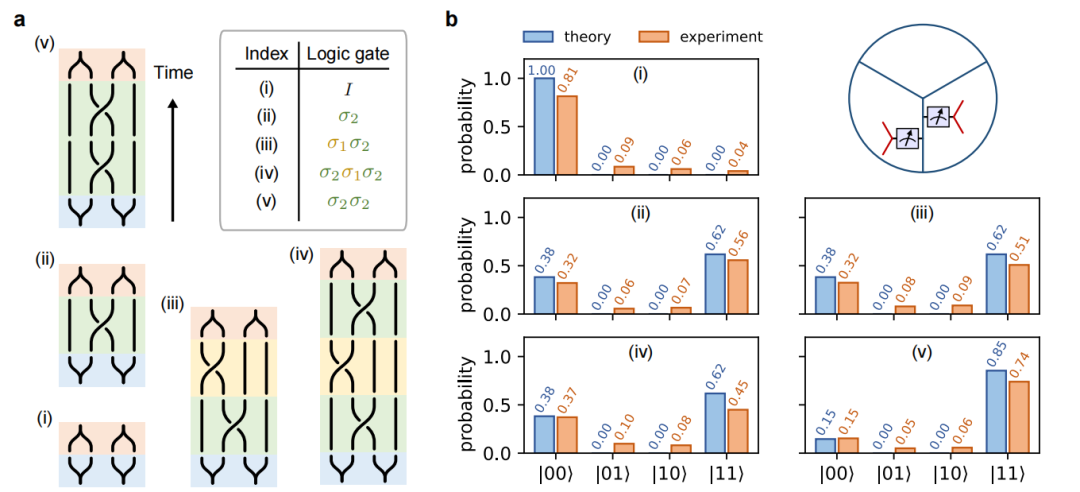
图3 以不同次序编织斐波那契任意子
作为拓扑量子计算领域重要的基础模型,斐波那契任意子的成功模拟与编织是实现通用拓扑量子计算的基础。该研究首次制备了斐波那契非阿贝尔拓扑态并实现了斐波那契任意子的编织操作,向最终实现通用拓扑量子计算迈出了重要一步。
该论文通讯作者为清华大学交叉信息研究院邓东灵助理教授,浙江大学物理学院王浩华教授和宋超研究员。浙江大学博士生徐世波、王可,交叉信息研究院博士后孙正之为文章共同一作。其他作者包括浙江大学超导量子计算团队部分其他成员,交叉信息研究院博士生李炜康、蒋文杰,以及南开大学陈省身数学研究所于立伟副研究员。该项目得到了国家自然科学基金委,科技部,合肥国家实验室,清华大学笃实专项、上海期智研究院等经费支持。
论文链接: https://www.nature.com/articles/s41567-024-02529-6