2024-05-24
Innovation Highlight
研究了具有收敛动力学的演化系统最优控制,使决策者在缺乏系统稳态反馈先验知识的情况下,能通过使用设计的“乐观-悲观收敛和置信界限算法 (OP-C2B)”,缩减学习与等待的时间,在带有期望约束的在线控制问题中同时实现亚线性的遗憾值和约束违背。该成果对设计和分析用于控制收敛动态系统的算法具有重要价值。
Achievements Summary
许多复杂系统对决策者的动作具有即时反馈,但其反馈需要较长时间才能收敛到稳态。这给没有先验知识的决策者带来了很大的困难,因为决策者需要精细地控制对系统收敛过程的探索与等待时长,从而保证学习精度与效率的平衡。这种动态系统的决策控制问题在许多现实领域中都可以观察到,如无线网络中的动态调度控制,多阶段的多智能体博弈等。
房智轩团队研究了具有收敛动力学的演化系统最优控制,使决策者在缺乏系统稳态反馈先验知识的情况下,能通过使用设计的“乐观-悲观收敛和置信界限算法Optimistic-Pessimistic Convergence and Confidence Bounds (OP-C2B)”,当等待某个动作接近稳态不值得时就迅速切换行动,来缩减学习与等待的时间。该算法通过利用“收敛界限”来确定系统离稳定状态有多远,并通过在维持对可行的动作集的悲观评估的同时在该集合内进行乐观动作选择来实现的。

图1. OP-C2B 算法
团队证明OP-C2B算法能够在有限动作集的情况下,保证亚线性的遗憾值和约束违背。特别地,当系统的收敛速率是线性或超线性时,OP-C2B可实现对数级的遗憾值和约束违背。此外,团队还将该算法推广到无限的决策者动作集,并证明了在移动众包和资源分配等重要的博弈控制场景中展示了算法的优越性。
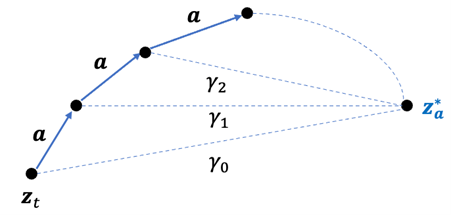
图2. 收敛动力学示意图
为算法提供了理论上的性能界限,对设计和分析用于控制收敛动态系统的算法具有重要价值。团队会在即将于6月举行的ACM SIGMETRICS (winter deadline 录用率10.2%) 会议上报告该项成果。
更多信息请阅读论文:
Learning the Optimal Control for Evolving Systems with Converging Dynamics, Qingsong Liu and Zhixuan Fang, Proceedings of the ACM on Measurement and Analysis of Computing Systems (POMACS), volume 8, 2024. (Accepted directly through ACM SIGMETRICS 2024 as the full version)
分享到