2024-08-23
The research group of Dongling Deng at the Institute for Interdisciplinary Information Sciences, Tsinghua University and Shanghai Qi Zhi Institue, in collaboration with the research groups led by Prof. Haohua Wang and Prof. Chao Song from the School of Physics at Zhejiang University, have created the long-sought-after non-Abelian Fibonacci topologically-ordered states and successfully simulated braidings of Fibonacci anyons for the first time with a programmable superconducting processor. Their paper, “Non-Abelian braiding of Fibonacci anyons with a superconducting processor”, was recently published in "Nature Physics."
Fundamental particles in nature are typically classified into bosons and fermions. The exchange of two such particles produces a phase of +1 (bosons, such as photons) or -1 (fermions, such as electrons) to the system wave function . This is due to the fact that in three-dimensional space, a path in which particle A circles around particle B (equivalent to swapping positions twice) can continually contract into a single point without passing through particle B. This restricts the system to return to its original quantum state after swapping particles twice. Therefore, swapping the particles will produce a phase factor of +1 or -1 each time. These particles are called bosons or fermions, satisfying the Bose-Einstein or Fermi-Dirac statistics. However, in two-dimensional space, the trajectory of particle A winding around particle B cannot continuously shrink to a single point without passing through particle B. In this case, the exchange of particles can produce an arbitrary phase, and these particles are referred as anyons. The process of particle exchange is called “braiding”. More generally, if the ground state is degenerate, the exchange of two particles can even change the amplitude of the system wave function, leading to the overall unitary evolution of the system rather than just acquiring a global phase. These types of particles are known as non-Abelian anyons.
The study of non-Abelian anyons is of crucial importance from both fundamental theory and potential application perspectives. Non-Abelian anyons differs from the conventional bosons and fermions in fundamental ways. They obey non-Abelian statistics and are building blocks for topological quantum computing, where the quantum gate operations are implemented by braidings of non-Abelian anyons, and the measurements are accomplished through anyon fusions. The topological properties of anyons make topological quantum computers inherently immune to local errors, providing fault tolerance at the hardware level.

Figure 1. An illustration of braiding Fibonacci anyons
Despite numerous theoretical proposals for realizing non-Abelian anyons with a wide range of systems, their experimental realization has remained challenging. With quantum processors, works on simulating non-Abelian anyons have emerged recently. However, none of the braidings of anyons realized in previous experiments alone sustain universal quantum computing. Fibonacci anyons have more complex statistical properties, making their experimental implementation even more challenging. They have a quantum dimension of the golden ratio, 1.618, and are closely related to the Fibonacci sequence in mathematics (see Figure 1). Their braiding is capable of realizing any quantum gate and can be used to build a universal fault-tolerant quantum computer.
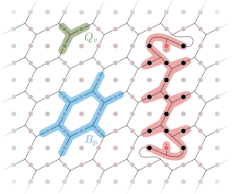
Figure 2. String-net model on a square lattice
Experimentally preparing the Fibonacci non-Abelian topologically-ordered states and implementing the braiding operation of Fibonacci anyons are widely believed to be extremely difficult. In this experiment, the string-net condensation model is adopted, where the qubits on the square lattice of the superconducting quantum processor match the honeycomb-shaped "strings" in the string-net model after a geometric transformation (see Figure 2). In this model, the Hamiltonian of the system is composed of the sum of all vortex operators Qv and all plaquette operators Bp. All strings are closed in the ground state, and Fibonacci anyons are distributed at both ends of the open strings in the excited state (see Figure 2). In this experiment, 27 superconducting qubits were used, and the median simultaneous single (double) qubit gate fidelity is 99.96% (99.5%). The non-Abelian Fibonacci topological ground state was prepared by a 115-layer quantum circuit.
After the preparation of the ground state, the topological entanglement entropy is measured, which agrees well with theoretical predictions. In particular, two pairs of Fibonacci anyons are generated through string operator manipulations on the prepared ground state and their braiding operations are demonstrated (Figure 3). A variety of different braiding sequences are designed in this experiment to test the characteristics of Fibonacci anyons (see Figure 3a), including: (i) Annihilation of Fibonacci anyons; (ii) Braiding changes the fusion results; (iii) and (iv) Verifying the Yang-Baxter equation with the same fusion results of two different braiding sequences; (v) Measurement of the quantum dimension of Fibonacci anyons. The experimental results were in excellent agreement with theoretical predictions (see Figure 3b). The quantum dimension of the Fibonacci anyon calculated from the experimental results of the braiding sequence (v) is 1.598, very close to the theoretical prediction of the golden ratio 1.618.
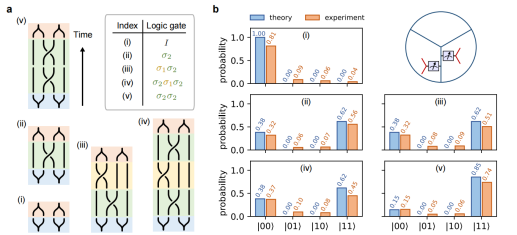
Figure 3. Braiding Fibonacci anyons with different sequences
As an essential model in the field of topological quantum computing, the successful simulation and braiding of Fibonacci anyons are the foundation for implementing universal topological quantum computing. This research is the first that has prepared a non-Abelian Fibonacci topologically-ordered state and implemented the braiding operations of Fibonacci anyons, making a significant step towards the ultimate realization of universal topological quantum computing.
The corresponding authors of this work include Prof. Dongling Deng at Institute for Interdisciplinary Information Science, Shanghai Qi Zhi Ibstitue, Prof. Haohua Wang and Prof. Chao Song from Zhejiang University. The co-first authors of the paper include Shibo Xu and Ke Wang (Ph.D. students at Zhejiang University) and Dr. Zheng-Zhi Sun (a postdoctoral fellow at the Institute for Interdisciplinary Information Sciences, Tsinghua University).
Other authors include members from the superconducting quantum computing team at Zhejiang University, Ph.D. students Weikang Li and Wenjie Jiang from Tsinghua, and Prof. Li-Wei Yu from the Chern Institute of Mathematics and LPMC at Nankai University. The research was funded by the National Natural Science Foundation of China, Innovation Program for Quantum Science and Technology, Tsinghua University Dushi Program and the Shanghai Qi Zhi Institute.