陈一镭

上海期智研究院PI，清华大学交叉信息研究院助理教授。

曾任VISA研究院研究员。于2018年获得波士顿大学计算机博士学位，本科毕业于上海交通大学。主要研究兴趣是密码学，特别是在伪随机，格密码，数论，和量子计算等方向。研究成果主要：设计了格问题的量子算法，建立了多线性映射和代码混淆在格问题上安全实现的基础，提出了证明Fiat-Shamir假设的方法，以及提出了一个不可逆群的构造。

后量子密码：研究加密、签名方案对抗量子计算机的安全性

密码学与复杂度理论：研究密码学的复杂性理论基础

成果3：关通过密码学方法来证明值域规避问题和远点问题的困难度（2024年度）

       最近在理论计算机领域对于显示构造问题的研究中，引入了一种系统性的方法，通过使用元问题（meta problems）来探索显式构造问题的复杂性，即值域规避问题（缩写为Avoid）和远点问题（缩写为RPP）。这些元问题的上限和下限为之前独立研究的特定显式构造问题的复杂性提供了统一的视角。以前的工作很大程度上未解决的一个有趣问题是：Avoid和RPP 对于简单电路（例如低深度电路）是否困难。

       陈一镭团队证明，在合理的密码学假设下，即使输入电路与常数深度电路一样简单，值域规避问题和远程点问题也无法通过非确定性搜索算法有效解决。这扩展了由 Ilango、Li 和 Williams (STOC’23) 针对采用 NP 见证加密（Witness encryption）的确定性算法建立的困难度结果，其中值域规避问题的输入是通用布尔电路。

       团队的主要技术贡献是一种新颖的见证加密结构，其灵感来自于 NP 中某些不太可能是 NP 完全的承诺语言（promise language）的公钥加密。团队引入了一种通用方法，将具有特定属性的公钥加密方案转换为与初始公钥加密方案相关的语言的见证加密方案。通过这种通用方法，团队提出基于标准格或基于编码的 PKE 方案的变体，团队在合理的假设下获得了 NP\ coNP/poly 中某些语言的可证明安全的见证加密方案。此外，陈一镭团队证明，在Rudich的超级比特（RANDOM'97）的广义安全概念下，陈一镭团队见证加密结构对于非确定性敌手来说也可能是安全的，这对于证明Avoid和RPP针对非确定性算法的难度至关重要。

论文信息：Hardness of Range Avoidance and Remote Point for Restricted Circuits via Cryptography，Yilei Chen, Jiatu Li

论文链接：https://eprint.iacr.org/2023/1894.pdf

------------------------------------------------------------------------------------------------------------------------------

成果2：关于S|LWE>问题的算法及复杂度证明（2023年度）

       “带错误学习问题”（LWE）是后量子密码学最重要的构建模块之一。 为了更好地理解 LWE 对于量子计算机的困难度，探索LWE 的量子变体，展示这些变体的量子算法，或证明它们与标准 LWE 一样困难至关重要。本文中深入研究了Chen、Liu 和 Zhandry 在[Eurocrypt 2022] 定义的一种LWE 的量子变体——S|LWE>问题。它将 LWE 样本的误差编码为量子幅度。在本文中，我们证明了新的S|LWE>困难度和算法。我们的主要结果是

       1. 如果S|LWE>具有未知相位的高斯幅度，那么它就和传统的LWE问题一样难；

       2. 如果S|LWE>具有已知相位的任意幅度，那么S|LWE>就具有亚指数时间量子算法。

       因此，如果我们能进一步改进以上两个结论的“未知相位”与“已知相位”的差距，就有可能设计出对于传统的LWE问题的亚指数时间量子算法。

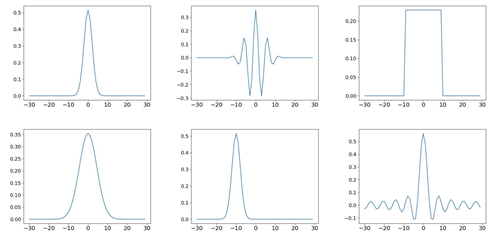
图为已知相位的高斯幅度、未知相位的高斯幅度、均匀随机幅度（上排从左到右）以及它们的傅立叶变换的图例（下排从左到右）

       研究领域：后量子密码学

       研究论文： On the Hardness of S|LWE> with Gaussian and Other Amplitudes. 

       Yilei Chen, Zihan Hu, Qipeng Liu, Han Luo, Yaxin Tu.  https://eprint.iacr.org/2023/1498 查看PDF

------------------------------------------------------------------------------------------------------------------------------

成果1：解决特殊格问题的量子算法（2022年度）

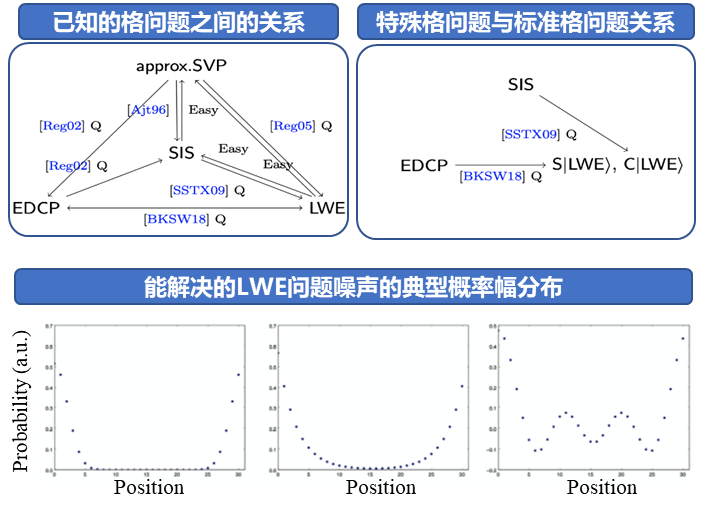
       寻找格上的最短向量一直被认为是计算机领域最困难的问题之一，至今没有经典或量子算法能在多项式时间内解决这个问题。因此构造基于格问题的密码一直被认为是构造防止量子计算机攻击的密码的有效途径之一。其中被用来构造公钥密码的SIS和LWE问题被证明和格上的最短向量问题是等价的。我院陈一镭团队和普林斯顿大学的刘启鹏和Mark Zhandry提出了一个能解决特殊格问题的多项式时间量子算法。这些特殊格问题是SIS和LWE的变种。他们虽然并不等价于标准的格问题，但是已经非常接近于密码学常用的问题。我们的量子算法中使用了一种被称为“过滤”的方法，是在量子算法的设计中第一次使用，可能为未来量子算法的设计带来新的思路。该成果以“Quantum Algorithms for Variants of Average-Case Lattice Problems via Filtering”为题发表于2022年欧洲密码大会（Eurocrypt 2022），并收到Journal of Cryptology邀稿。