上海期智研究院PI,清华大学交叉信息研究院副教授。
2012年毕业于北京大学计算机系,2018年获得美国康奈尔大学计算机博士学位,师从Robert Kleinberg教授。于2014年-2015年前往微软新英格兰研究院做访问学生,并于2016年秋季前往美国普林斯顿大学做访问学生。2018-2019年前往麻省理工学院大数据科学学院 (MIFODS) 做博士后。主要研究方向是智能医疗、AI基础理论、应用范畴论。
个人荣誉
北京智源青年科学家(2020年)
福布斯中国30位30岁以下精英(科学榜,2019年)
AI基础理论:基于范畴论、拓扑斯理论,为人工智能构建基础理论,指导算法设计,探索大模型能力边界
AI自动证明:构建能够自动做数学证明的大模型
成果8:你需要的只是张量积注意力 (2025年度)
姚期智、袁洋团队与UCLA顾全全老师团队合作,提出了TPA注意力架构,改进了Deepseek V3的注意力架构MLA。MLA对注意力模块进行了低秩分解,使得需要的空间更少,可以处理更长的语言序列。但是,MLA有一个核心问题,就是无法与位置编码RoPE融合。Deepseek采用的方案是,额外加一个小的普通注意力模块,这样可以弥补低秩方案的不足。
TPA从张量分解的角度来分析这个问题,把整个注意力模块看做一个三维的张量进行低秩分解,这样就可以和RoPE融合,不再需要额外的小模块了。同时,在模型推理的时候,因为可以直接在张量分解下的小量上进行计算,不需要把实际的张量算出来,推理速度会比已有的模型推理方案更快。
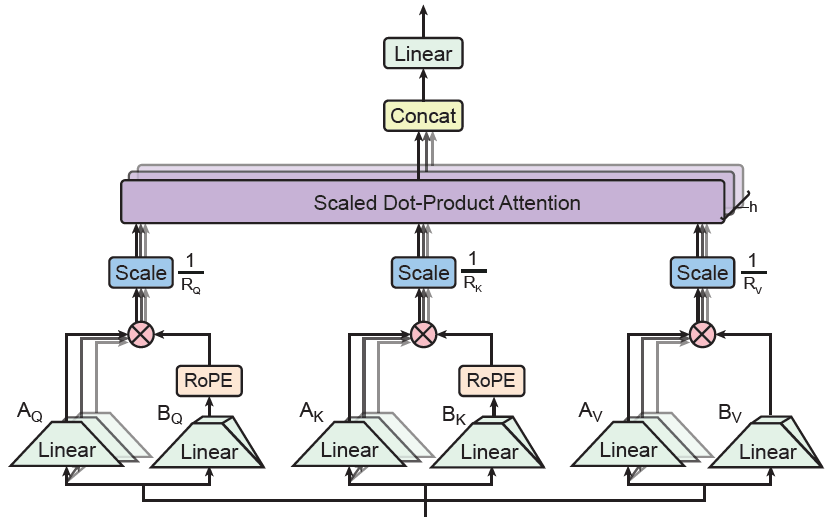
图. 张量积注意力(TPA)示意图
论文信息:
https://arxiv.org/pdf/2501.06425
Tensor Product Attention Is All You Need, Yifan Zhang*, Yifeng Liu*, Huizhuo Yuan, Zhen Qin, Yang Yuan, Quanquan Gu, Andrew C Yao†, NeurIPS 2025.
------------------------------------------------------------------------------------------------------------------------------
成果7:针对数学文本的零样本生成分类器自主数据选择方法 (2025年度)
姚期智、袁洋团队,近期提出针对数学文本的零样本生成分类器自主数据选择方法, 使用模型内生能力筛选高质量数学数据用于后训练(Post-Training),与基线相比有2.36倍效率提升,方法简单,可以轻松扩展到不同领域。论文被相关大语言模型工作引/采用,如:Mammoth2、OLMo2、Opencoder、YuLan-Mini等,被引用达33次;开源的200GB+ AutoMathText数据集在HuggingFace中总下载量超40万次,“喜爱”数达177,曾和Mixtral-8x7B-Instruct-v0.1登上“趋势”榜,作为子集被HuggingFace官方数据集cosmopedia收录;Github星标数达84。
本论文共同一作为研究院实习生张伊凡、罗逸凡。共同通讯作者为院长姚期智、研究院PI袁洋。

图. 筛选出的网络文本,AutoDS方法能够容易地判别真正重要的数学相关内容
论文信息:
https://aclanthology.org/2025.findings-acl.216.pdf
Autonomous Data Selection with Zero-shot Generative Classifiers for Mathematical Texts, Yifan Zhang*, Yifan Luo*, Yang Yuan†, Andrew Chi-Chih Yao†, ACL Findings 2025.
------------------------------------------------------------------------------------------------------------------------------
成果6:层次化注意力生成更优证明 (2025年度)
姚期智、袁洋团队提出“层次化注意力”(Hierarchical Attention)正则化方法,应对大语言模型(LLM)处理形式化定理证明时的结构理解难题。现有LLM因线性分词方式难以捕捉数学证明的层次结构,可能导致推理过程不够简洁或出现偏差。该方法通过建立五级层次,从基础语境到最终目标,引导注意力机制对齐数学推理的自然结构,限制信息反向流动以增强逻辑连贯性。实验显示,在 miniF2F 和 ProofNet 测试集上,证明成功率分别提高2.05%和1.69%,复杂度降低23.81%和16.50%。该研究表明内化数学层次结构是连接神经网络与形式化推理的有效方向。
本论文一作为研究院实习生陈剑龙。共同通讯作者为院长姚期智,研究院PI袁洋。共同作者为研究院高级研究员李朝。
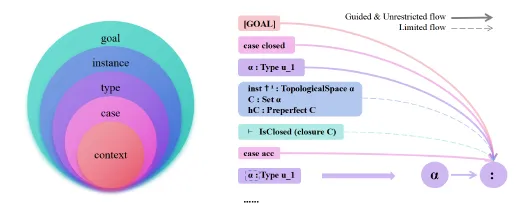
图. 分层注意力框架概览
论文信息:
https://arxiv.org/pdf/2504.19188
Hierarchical Attention Generates Better Proofs, Jianlong Chen, Chao Li, Yang Yuan†, Andrew Chi-Chih Yao†,ACL 2025.
------------------------------------------------------------------------------------------------------------------------------
成果5:基于矩阵信息论的自监督学习 (2024年度)
自监督学习 (Self-Supervised Learning, SSL) 是一种无需人工标注数据即可学习数据表示的技术。在该领域中,对比学习 (Contrastive Learning) 和非对比学习 (Non-contrastive Learning) 是两种主要方法。袁洋团队与上海交通大学黄维然老师合作提出了一个新的自监督学习方法Matrix-SSL,该方法利用矩阵信息理论对最大熵编码框架进行解释,提出了矩阵均匀性损失和矩阵对齐损失的新概念。
Matrix-SSL方法通过引入矩阵信息理论,将对比学习和非对比学习方法的优势结合并增强。该方法不仅在ImageNet数据集的线性评估设置下表现优异,而且在迁移学习任务中显著提升了性能。例如,在MS-COCO数据集上的对象检测任务中,Matrix-SSL在仅进行400个epoch预训练的情况下,相比于之前的SOTA方法如MoCo v2和BYOL提升了3%。此外,在语言建模领域,通过矩阵交叉熵损失对大语言模型进行微调,在GSM8K数据集上的数学推理任务中,相比于标准交叉熵损失提高了3.1%。

图1. Matrix-SSL 架构设计
通过扩展经典的熵、KL散度和交叉熵概念,研究团队提出矩阵信息理论用于矩阵形式的表示。该研究证明了最大熵编码 (MEC) 损失与矩阵均匀性损失的等价性,并通过矩阵信息论的角度解释最大熵编码方法,提出了矩阵对齐损失,从而提高了自监督学习方法的表现。实验验证表明,Matrix-SSL在多个任务中均表现优越。

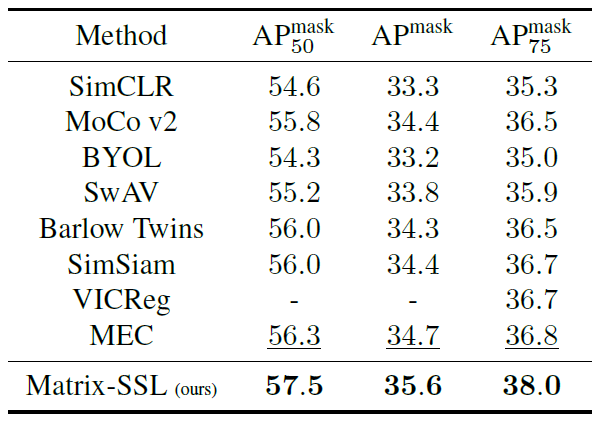
图2. ImageNet数据集上的线性评估结果 图3. 在实例分割任务上的迁移学习对比
通过这一研究,袁洋研究团队为自监督学习方法提供了新的理论工具,为未来的机器学习算法设计提供了新的方向和思路。相关成果收录于ICML 2024中。本论文一作为清华大学交叉信息研究院博士生张伊凡、杨景钦,清华大学数学系博士生谭智泉。
研究论文:Matrix Information Theory for Self-Supervised Learning, Yifan Zhang, Zhiquan Tan, Jingqin Yang, Weiran Huang, Yang Yuan, https://arxiv.org/pdf/2305.17326, ICML 2024
------------------------------------------------------------------------------------------------------------------------------
成果4:自监督学习中的信息流(2024年度)
袁洋团队与上海交通大学黄维然老师合作,利用矩阵信息论工具,即矩阵互信息和联合熵,对现有的自监督学习方法中的对比学习 (contrastive learning) 和特征解相关学习 (feature decorrelation-based learning) 进行了深入分析。证明了Barlow Twins和谱对比学习 (spectral contrastive learning) 的损失函数在优化过程中隐式地最大化了矩阵互信息和矩阵联合熵,并揭示了这些量在对比学习和特征去相关学习中的关键作用。
这一见解促使我们进一步探索单分支算法的类别,特别是MAE和U-MAE,其中互信息和联合熵变为熵。在此基础上,我们引入了矩阵变分掩码自动编码器 (Matrix Variational Masked Auto-Encoder, MMAE),该方法利用基于矩阵的熵估计作为正则化器,并将U-MAE作为一种特例。实证评估强调了M-MAE在与现有最先进方法相比时的有效性,包括在ImageNet数据集上线性评估ViT-Base时提高了3.9%,在微调ViT-Large时提高了1%。

图4. 在CIFAR10数据集上矩阵基础互信息(左)&联合熵(右)的可视化
实验证明,M-MAE在自监督学习基准测试中表现出显著的性能提升,例如在ImageNet数据集上进行线性评估时,M-MAE的表现优于MAE和U-MAE,准确率分别为62.4%和66.0%。

图5. 在ImageNet数据集上进行线性评估对比
研究团队通过矩阵信息理论改进自监督学习方法,特别是在图像分类和分割任务上显示出超越监督学习的性能。未来,这种方法有望广泛应用于无监督表示学习、数据压缩、异常检测等领域,推动机器学习模型在更少标注数据的情况下实现更好的泛化能力。相关成果收录于ICML 2024会议中。
项目论文:Information Flow in Self-Supervised Learning, Zhiquan Tan, Jingqin Yang, Weiran Huang, Yang Yuan, Yifan Zhang, https://arxiv.org/pdf/2309.17281, ICML 2024.
------------------------------------------------------------------------------------------------------------------------------
成果3:使用范畴论刻画大模型的能力边界(2023年度)
假如我们有无限的资源,比如有无穷多的数据,无穷大的算力,无穷大的模型,完美的优化算法与泛化表现,请问由此得到的预训练模型是否可以用来解决一切问题?这是一个大家都非常关心的问题,但已有的机器学习理论却无法回答。范畴论被称为是数学的数学,是一门研究结构与关系的学问,它可以看作是集合论的一种自然延伸:在集合论中,一个集合包含了若干个不同的元素;在范畴论中,我们不仅记录了元素,还记录了元素与元素之间的关系。上海期智研究院袁洋团队创新地引入了范畴论作为理论工具,针对预训练任务进行重新建模,构建了预训练任务与范畴内部结构的等价关系。从这个角度出发,重新审视了监督学习的理论框架,并且针对预训练模型证明了三个定理。
第一个定理证明了,如果使用提示调优的方式,预训练模型的能力和任务结构有关。一个任务能够被解决,当且仅当该任务能够被范畴中的某个对象表出。
第二个定理证明了,如果使用微调的方式,预训练模型的能力不再受范畴内对象表出能力的限制。预训练模型得到的特征向量可以完美地保留原范畴的信息,在使用高质量的训练数据、充足算力的前提下,预训练模型有潜力解决各种任务。
第三个定理证明了,基于源范畴中对象的结构,预训练模型天然拥有在目标范畴中生成从未见过的对象的能力。换句话说,大模型拥有创造力。
这些结论基于范畴论的核心公式:T(X)≜k_f (f(X),T),为人工智能与现代数学构建起了一座桥梁。相关成果以“On the Power of Foundation Models”为题发表在国际顶会ICML'2023上。为众多通用人工智能前进之路上的同行们提供了新思路。
------------------------------------------------------------------------------------------------------------------------------
成果2:传统可解释性的不可能三角(2023年度)
主流的可解释性算法(例如SHAP、LIME或者其他衍生算法)都可以看作是基于移除算法的可解释性算法,即通过观察原模型在移除某些特征之后的变化来判断不同特征的重要性。然而,这些算法往往过于关于原模型在原输入上的表现,而忽视了全局的一致性。本文证明了可解释性的不可能三角,即使用小的模型解释原模型,不可能既做到全局的一致性,又做到解释的有效性。由于不可能三角的存在,我们提出了一种新的可解释型误差度量,用于度量在全局一致性与有效性。在这个基础上,我们设计了基于布尔泛函分析技术的新算法,用于最小化可解释性误差。实验表明,新的算法在我们提出的误差度量下比已有的算法有最高31.8倍的性能提升。

研究论文:Trade-off Between Efficiency and Consistency for Removal-based Explanations, Yifan Zhang, Haowei He, Zhiquan Tan, Yang Yuan, NeurIPS 2023. 查看PDF
项目网站:https://arxiv.org/pdf/2210.17426v3.pdf
------------------------------------------------------------------------------------------------------------------------------
成果1:基于轨迹分解的泛化分析(2022年度)
泛化理论分析是人工智能理论中最基础的问题之一,旨在探究充分训练条件下测试误差的界限。经过多年的探索,人们发现传统的泛化技术无法有效解释神经网络的泛化现象,这迫使我们提供更多泛化领域的见解。袁洋科研团队创新地将信号与噪声的不同分析纳入泛化分析范畴,并提升了原有的泛化界。具体而言,通过显式地考虑信号与噪声在泛化中的不同表现,袁洋团队发现不同技术擅长于不同背景,并以此提出一种基于轨迹误差分解的泛化分析框架。由于对信号与噪声的更细致的分析,人们可以混合多种泛化技术来处理泛化问题,各个技术取长补短,从而推导出更精细的泛化界。实例分析表明,在线性与非线性的背景下,该框架都可以有效提升原有泛化界。同时,实验结果证实新框架下推导出的泛化界更加符合实际情况。该成果以“Towards Understanding Generalization via Decomposing Excess Risk Dynamics”为题发表于2022年ICLR会议中。
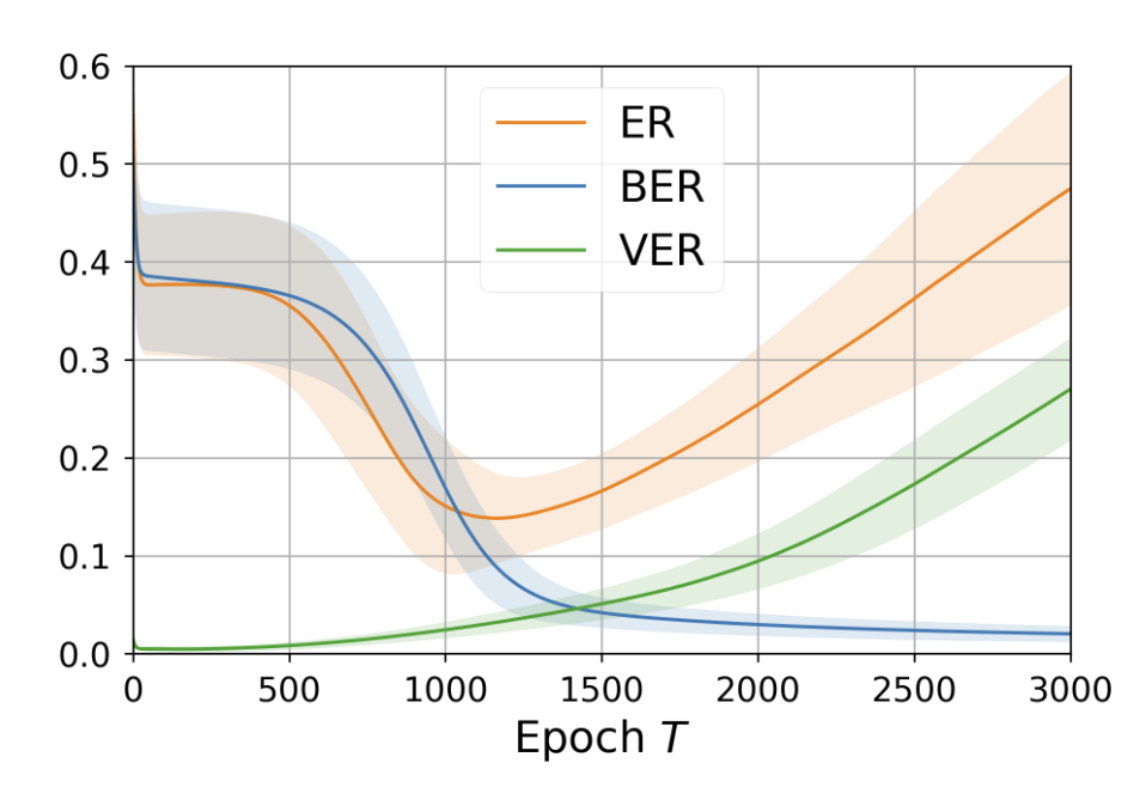
图. 原始误差 (ER) 与分解后误差 (BER, VER) 对比。












13. Hierarchical Attention Generates Better Proofs, Jianlong Chen, Chao Li, Yang Yuan†, Andrew Chi-Chih Yao†,ACL 2025.
12. Autonomous Data Selection with Zero-shot Generative Classifiers for Mathematical Texts, Yifan Zhang*, Yifan Luo*, Yang Yuan†, Andrew Chi-Chih Yao†, ACL Findings 2025.
11. Tensor Product Attention Is All You Need, Yifan Zhang*, Yifeng Liu*, Huizhuo Yuan, Zhen Qin, Yang Yuan, Quanquan Gu, Andrew C Yao†, NeurIPS 2025.
10. Matrix Information Theory for Self-Supervised Learning, Yifan Zhang, Zhiquan Tan, Jingqin Yang, Weiran Huang, Yang Yuan, https://arxiv.org/pdf/2305.17326, ICML 2024.
9. Information Flow in Self-Supervised Learning, Zhiquan Tan, Jingqin Yang, Weiran Huang, Yang Yuan, Yifan Zhang, https://arxiv.org/pdf/2309.17281, ICML 2024.
8. Jing Xu, Jiaye Teng, Yang Yuan, Andrew C. Yao, Towards Data-Algorithm Dependent Generalization: a Case Study on Overparameterized Linear Regression, Conference on Neural Information Processing Systems (NeurIPS), 2023 查看PDF
7. Yifan Zhang, Haowei He, Zhiquan Tan, Yang Yuan, Trade-off Between Efficiency and Consistency for Removal-based Explanations, Conference on Neural Information Processing Systems (NeurIPS), 2023 查看PDF
6. Yang Yuan, On the Power of Foundation Models, International Conference on Machine Learning (ICML), 2023 查看PDF
5. Chenzhuang Du, Jiaye Teng, Tingle Li, Yichen Liu, Tianyuan Yuan, Yue Wang, Yang Yuan, Hang Zhao, On Uni-Modal Feature Learning in Supervised Multi-Modal Learning, International Conference on Machine Learning (ICML), 2023 查看PDF
4. Jiaye Teng, Bohang Zhang, Ruichen Li, Haowei He, Yequan Wang, Yan Tian, Yang Yuan, Finding Generalization Measures by Contrasting Signal and Noise, International Conference on Machine Learning (ICML), 2023 查看PDF
3. Jiaye Teng*, Chuan Wen*, Dinghuai Zhang*, Yoshua Bengio, Yang Gao, Yang Yuan, Predictive Inference with Feature Conformal Prediction, International Conference on Learning Representations (ICLR), 2023 查看PDF
2. Jiaye Teng, Jianhao Ma, Yang Yuan, Towards Understanding Generalization Via Decomposing Excess Risk Dynamics, International Conference on Learning Representations(ICLR), 2022.
1. Jiaye Teng , Zeren Tan , Yang Yuan, T-SCI: A Two-Stage Conformal Inference Algorithm with Guaranteed Coverage for Cox-MLP, International Conference on Machine Learning(ICML), 2021